
So, if any one of the acute angles is given, then we can easily find the third angle by subtracting the given acute angle from 90. To find the side of the triangle, we need the sides of other two triangle. In a right scalene triangle, the sum of both the acute angles is 90° and the third angle is equal to 90°.
#Area of right isosceles triangle formula using hypotenuse how to#
How to Find the Angles of a Right Scalene Triangle? All the three angles of a right scalene triangle are different in measurement.


What does a Right Scalene Triangle Look Like?Ī right scalene triangle looks like a right triangle with two perpendicular sides forming an angle of 90 degrees. This formula is known as the Pythagoras theorem. To find the length of the hypotenuse, we need to use the following formula which expresses the relation between three sides of a right scalene triangle: Hypotenuse 2 = Perpendicular 2 + Base 2. The hypotenuse is the longest side of a right triangle which is opposite to the 90-degree angle. How to Find the Hypotenuse of a Right Scalene Triangle? Then, we can simply join the opposite ends of both to form a right scalene triangle. To draw a right scalene triangle, the first step is to draw two perpendicular line segments of different measurements. The perpendicular of the right scalene triangle can be taken as the height and the side adjacent to it other than hypotenuse is the base. The area of a scalene right triangle can be calculated by using the formula: Area = 1/2 × base × height. What is the Area of a Right Scalene Triangle? One of its angles measures 90°and all the sides and angles are different in measurements.
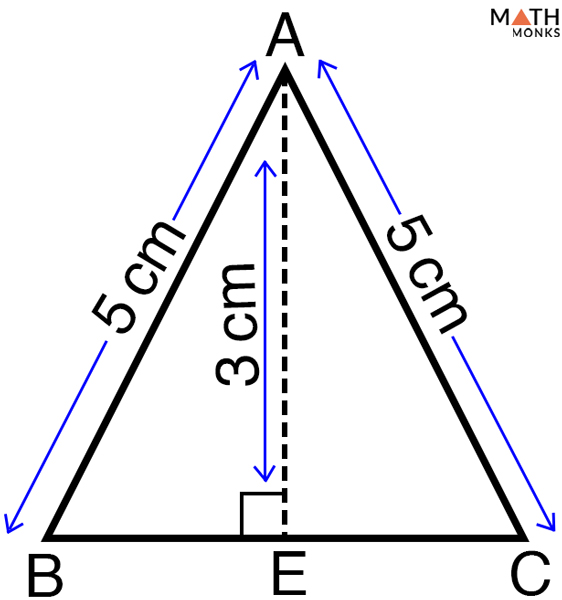
It comes in the category of both right triangles and scalene triangles. Hence, the length of the other side is 5 units each.FAQs on Right Scalene Triangle What is a Right Scalene Triangle?Ī right scalene triangle is a triangle that contains the properties of both the right triangle and scalene triangle. Ques: Find the length of the other two sides of the isosceles right triangle given below: (2 marks)Īns: We know the length of the hypotenuse is \(\sqrt\) units In the right isosceles triangle, since two sides (Base BC and Height AB) are same and taken as ‘B’ each. The Sum of all sides of a triangle is the perimeter of that triangle. If, base (BC) is taken as ‘B’, then AB=BC=’B’ This applies to right isosceles triangles also.Īs stated above, in an isosceles right-triangle the length of base (BC) is equal to length of height (AB). The area of a triangle is half of the base times height. Pythagoras theorem states that the square of the hypotenuse of a right triangle is equal to the sum of the square of the other two sides. If base (BC) is taken as ‘B’, then AB=BC=’B’.
In an isosceles right triangle, the length of base (BC) is equal to length of height (AB). Pythagoras theorem, which applies to any right-angle triangle, also applies to isosceles right triangles. Given below are the formulas to construct a triangle which includes: And AB or AC can be taken as height or base Problem: Finding the hypotenuse of a right. Since multiplying these two values together would give the area of the corresponding rectangle, and the triangle is half of that, the formula is: area ½ × base × height. In a right triangle, the base and the height are the two sides that form the right angle. Let us solve some problems to understand the concept better. All that you need are the lengths of the base and the height. The above formula is also written as, c a 2 + b 2, here c hypotenuse, a height, b base. This type of triangle is also known as a 45-90-45 triangleĪC, the side opposite of ∠B, is the hypotenuse. Thus, mathematically, hypotenuse is the sum of the square of base and height of a right triangle. In an isosceles right triangle (figure below), ∠A and ∠C measure 45° each, and ∠B measures 90°. A triangle in which one angle measures 90°, and the other two angles measure 45° each is an isosceles right triangle.


 0 kommentar(er)
0 kommentar(er)
